26 October 2024
 https://www.researchgate.net/publication/357386257_Imposing_Contiguity_Constraints_in_Political_Districting_Models
https://www.researchgate.net/publication/357386257_Imposing_Contiguity_Constraints_in_Political_Districting_ModelsOur previous article implores academic researchers to publish data and code to accompany their papers. We use an example where academic publishing has been done well: with papers about creating voting districts accompanied by data and models available on Github.
On a related topic, Alireza Soroudi has published an article on LinkedIn describing a Gerrymandering using Constraint Programming model. Dr. Soroudi's model has the specific objective of showing how electoral district boundaries can be manipulated to advantage a party, group, or socioeconomic class within the constituency. As Dr. Soroudi says:
Gerrymandering – the crafty art of redrawing electoral districts to tip the scales in favor of a particular party – is as intriguing as it is controversial.
In this article, we take a simple approach to modifying a redistricting model. We add a requirement to our model that could be interpreted as either:
- The laudable goal of grouping together "communities of interest" – a common requirement when designing voting districts; or
- A nefarious attempt to manipulate the electoral outcome by gerrymandering.
Gerrymandering is the opposite of the model's purpose in our previous article. But, as model designers, we need to be aware that we don't always control the purposes to which decision makers apply our models and decision makers don't always understand the implications of small changes to a model.
Download the models
We make a minor change to the model described in our previous article, which is built in Python, using the Pyomo library.
The files are available on GitHub.
Situation
As described in our previous article, we have "the task of partitioning a state into geographic-based districts for election purposes". Design of political districts generally requires compliance with multiple criteria, including equal population (within tolerances), contiguity, communities of interest, etc. Political districting models may be used to reduce the problems associated with partisan gerrymandering.
Our previous model doesn't explicitly account for communities of interest, so we add that feature in this article. That is, we add the requirement that, where possible, rural and urban counties are combined into different districts. There could be different motivations for why we define rural and urban counties as separate communities of interest – we'll return to the motivation later in this article.
Original redistricting plan
We use the example of the USA state of Oklahoma. The state consists of 77 counties that we need to aggregate into 5 districts, each of which is required to be compact, contiguous, and have approximately equal population.
The population of each county is illustrated in Figure 1. There are only five counties with a population over 100,000 people, which we define as urban counties. All other counties are defined as rural. That is:
- Oklahoma County, population 796,292.
- Tulsa County, population 669,279.
- Cleveland County, population 295,528.
- Canadian County, population 154,405.
- Comanche County, population 121,125.
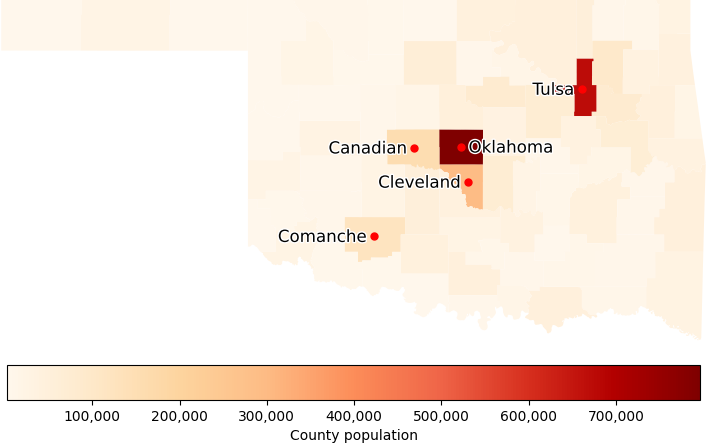
We are required to create five districts of approximately equal population – meaning within ±1% of the total state population divided by the number of districts. Our data says that Oklahoma state has a total population of 3,959,353. Therefore, each of the 5 districts must have a population between 783,952 and 799,789.
Using the model from our previous article, we obtain the solution shown in Figure 2.
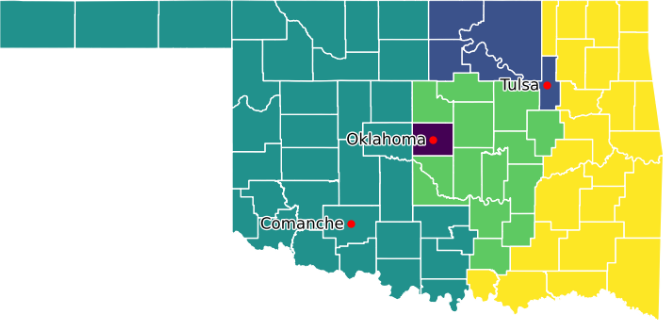
Fortunately, Oklahoma County's population is within the required district population range, so it is a district by itself. Tulsa plus a few rural counties form a district. Of the other three urban counties, Comanche County and Canadian County are in the same district, while Cleveland County is in another district.
Revised redistricting plan
We could argue that urban counties that are geographically close should be grouped together as communities of interest, where possible. This is on the basis that urban voters have more issues in common with each other than with their rural neighbours. Therefore, it is reasonable for them to be represented together in political forums. Similarly, rural voters should be grouped together to better represent their shared political issues.
Considering this requirement, the original redistricting plan is not ideal. Given their populations, Oklahoma County and Tulsa County must be in different districts and cannot be combined with other urban counties. But Cleveland County, Canadian County, and Comanche County could be combined into the same district, as their combined population of 571,058 leaves room for adding a few rural counties to comply with the district population bounds.
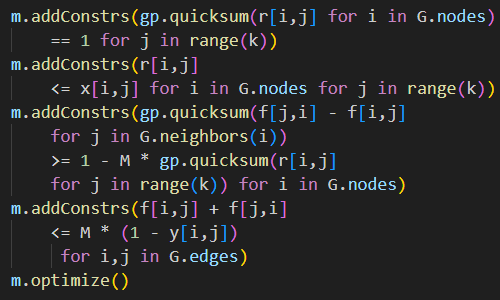
To represent urban and rural communities of interest, we could add constraints to the model for combining communities of interest into districts. But, as a special case, we can achieve the same result by simply specifying that Cleveland County, Canadian County, and Comanche County must be in the same district. We do that by adding the constraints shown in Figure 3 to the create_model function.
model.same_district_08_10 = pyo.Constraint(model.districts,
rule=lambda model, j: model.assign[8, j] == model.assign[10, j])
model.same_district_08_47 = pyo.Constraint(model.districts,
rule=lambda model, j: model.assign[8, j] == model.assign[47, j])
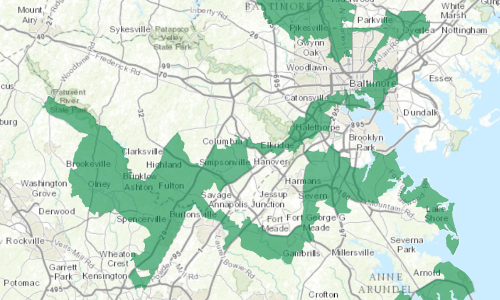
The result of this small change in the model's constraints is shown in Figure 4. We have 5 districts that each comply with the population bounds and other constraints. The districts are not quite as compact as the original design, but they're not unreasonable. Importantly, these districts meet our communities of interest goal with Oklahoma County as one district, Tulsa the basis of a district, the other three urban counties in the same district, and all the other rural counties grouped into two districts.
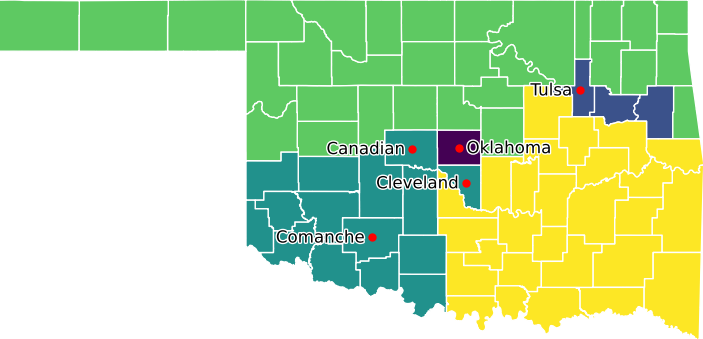
Which districting plan should we accept?
Our revised districting plan in Figure 4 is quite different from the original plan in Figure 2. Which plan should we accept? The answer depends on the motivation for adding community of interest constraints to the model.
Suppose that historical voting is such that urban voters tend to vote for the Urban Party and rural voters tend to vote for the Rural Party. In the original allocation of counties to districts, the majority of voters in the Oklahoma County and Tulsa County districts are urban, so the Urban Party will likely win those districts. The district containing Comanche and Canadian Counties has a majority of rural voters, so the Rural Party will likely win that district. The other two districts are overwhelmingly rural, even with the inclusion of Cleveland County, so the Rural Party wins those districts. The result is that the Urban Party wins 2 districts and the Rural Party wins 3 districts, so the Rural Party wins Oklahoma State overall.
But combining the Comanche, Canadian, and Cleveland Counties into the same district gives that district a majority of urban voters, so the Urban Party wins that district. The winners of the other districts remain unchanged. The result is that the Urban Party wins 3 districts and the Rural Party wins 2 districts, so the Urban Party wins Oklahoma State overall.
By adding the community of interest requirement, we flipped the winner of the state election. We argue that urban and rural voters should be represented as separate communities of interest. If that argument is accepted, then the revised districting plan is better. But if our motivation is to skew the voting outcome in favour of the Urban Party, then the community of interest requirement should be rejected. We'll leave it to you to decide one way or the other.
Conclusion
In this article, we add a simple community of interest requirement to the political redistricting model described in our previous article.
We argue that rural and urban voters are separate communities of interest, so districts should be designed around those communities. In our example, this community of interest requirement changes the balance of power in one of the districts, potentially leading to a different winner in the state election.
Whether or not the potential change in outcome is acceptable depends on your assessment of the community of interest requirement and the details of our implementation. Is the change motivated by a genuine desire to aggregate legitimate communities of interest, or is it motivated by a nefarious attempt to gerrymander the result?
Understanding the motivations of decision makers can be difficult. When developing a model, we need to be aware of how different modelling approaches and small implementation details may change the result. We must consider whether the changes are intended or unintended. We must also ensure that the decision makers are properly informed about the impact of changes when using our models.
If you would like to know more about this model, or you want help with your own models, then please contact us.