29 January 2022
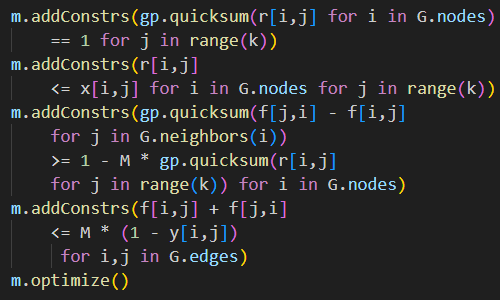
When formulating a model, many of the problems we encounter involve non-linear formulae. For example, a fixed cost is incurred only if a facility is built, or a variable can take values only in the ranges 5 to 10 or 80 to 100.
Optimization models work best when the objective function and constraints are all linear. In some situations, it is possible to reformulate a model to linearize the non-linear parts. The techniques for linearizing non-linear formulae can make the difference between a model being viable or not.
FICO Xpress Optimization have written a booklet that describes a variety of useful mixed-integer programming (MIP) formulations and linearizations, including:
- Binary variable logical conditions.
- Minimum, maximum, and absolute value of binary variables.
- Multiplication of variables.
- Variables with disjunctions.
- Batch sizes.
- Minimum activity level.
The booklet is available at: MIP formulations and linearizations.