5 January 2024

In our previous article, we solved a mixed integer linear program (MILP) model with more than 8 million binary variables. Not long ago, a model of that size would have been unsolvable. Yet, once we had a computer with sufficient memory, the model was solved to optimality by an open source solver in 3 hours.
Of course, not all large models are solvable – even some small models are unsolvable, or at least hard to solve. Nonetheless, modern solvers, in association with modern computers, enable us to solve models that not-so-long-ago were beyond our capabilities.
In our next article, we look to compile crosswords using a MILP model. We're not the first to consider using a MILP model to compile crosswords. An article published in 1989 reported attempts to compile small crosswords using MILP models. The article's conclusion was very pessimistic, noting that:
...the prospects of using integer programming for any type of puzzle of realistic size and with a substantial lexicon remain bleak.
Wilson, 1989, Crossword compilation using integer programming
The problems Wilson encountered were insufficient computer memory and the time needed to solve a very small crossword grid, even though he was using a then state-of-the-art million dollar superminicomputer.
But a lot has changed in the 35 years since 1989. Computer hardware is many times faster, and memory capacity has increased enormously. In addition, optimization solver software has improved by orders of magnitude. Models that were difficult to solve in 1989 are now trivial. Solutions that were impossible to find in 1989 may now be within reach.
In this article, we estimate the magnitude of speed improvement for optimization solvers and computer hardware in the 35 years from 1989 to 2024. The results may be surprising.
1989: Crossword compilation using integer programming

As a motivating example, we consider an early attempt to compile crosswords using a mixed integer linear program (MILP). The paper Crossword compilation using integer programming, was published in 1989 by J. M. Wilson. That article proposes two MILP model formulations for compiling crosswords:

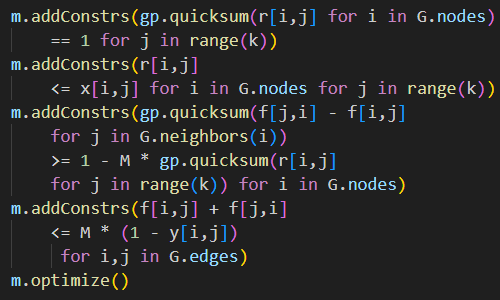
- Model 1, whole words. Model 1 attempts to fit whole words into a 4x4 fully interlocking puzzle (i.e. no black cells), as shown in Figure 1. With a lexicon of 100 4-letter words, the problem size was 800 variables and 524 constraints. A solution for this 4x4 double word square puzzle was found in 1,800 seconds.
- Model 2, individual letters. Model 2 attempts to place individual letters into a grid. It is more memory-efficient than Model 1, but it failed to find any solutions within 3,000 seconds, even for very small grids. In any case, Model 2 has a loose formulation that can create "words" that are not in the lexicon, so a solution (if found) may not be valid.
From Wilson's experience, we observe that:
- A key modelling issue was memory usage, especially as the lexicon size increases. The models used a lexicon of 100 words, which is very limiting given that there are several thousand 4-letter English words.
- Solutions were difficult to find, even for very small grids.
- A model with 800 variables and 524 constraints is now considered to be small. In 1989 it was a large model.
- Dense American-style puzzles (like Figure 1) are much harder to solve than sparser British-style crossword puzzles. This is likely because a dense grid has more word intersections. We'll explore this issue further in our next article.
- The modelling was performed on a Prime 750 superminicomputer, an example of which is shown in Figure 2. The Prime 750 superminicomputer had up to 8 MB of RAM and it ran at 1 million instructions per second (MIPS). The Prime 750 was a state-of-the-art computer at the time. Depending on configuration, a system cost several hundred thousand US dollars in the mid to late 1980s. That equates to about US$1,000,000 today, adjusted for inflation.
Wilson's paper refers to another paper that uses a lexicon of 1,000 4-letter words to compile crosswords using first-order predicate logic in the Prolog programming language, noting that, "This size of lexicon would present an almost impossible task for an integer programming model."
Overall, Wilson was pessimistic about using integer programming for compiling crosswords, considering it to be impractical, concluding that "the prospects of using integer programming for any type of puzzle of realistic size and with a substantial lexicon remain bleak".
So, integer programming was not a viable method for compiling crossword puzzles in 1989. But a lot has changed since then.
Computers and solvers have improved enormously
Wilson's paper was published in 1989. As we write this article in early 2024, that's 35 years ago. Since 1989, computers have become much faster, and they have a lot more memory. In addition, linear programming solvers have improved in both speed and sophistication.
In the following sections we attempt to estimate the magnitude of improvement in the 35 years since 1989.
Computer improvements
Computer speed improvement: 1989-2024
Computer processing speed has increased enormously over time. According to the 50 years of microprocessor trend data shown in Figure 3, single-thread Computer Processing Unit (CPU) performance (using the SpecINT benchmark) improved from an average score of 67 in 1988-1989 to 105,300 in 2021. That equates to a factor of 1,572 times faster.
From 2021 to 2023, CPU single thread benchmark scores improved by a further 10%, for a total factor from 1989 to 2023 of 1,729 times faster.

Until 2004, almost all CPUs had a single processing core. Since then, the number of logical CPU cores (i.e., physical cores and/or parallel threads within a physical core) has been increasing. A typical desktop computer now has at least several cores, with many having one or two dozen cores. Some CPUs have hundreds of cores. Graphics card GPUs typically have thousands of cores, though that is a different story.
Many solvers can use multiple CPU cores, to a greater or lesser extent. For example:
- Gurobi and CPLEX use multiple cores, by default, when solving models.
- The Octeract solver engine relies on parallel processing for its high performance in solving non-linear models.
- The open-source HiGHS solver has "limited opportunities for exploiting parallel computing", though greater use of multiple CPU cores is planned soon.
However, the speed improvement for multiple cores compared with a single core, according to Amdahl's law, is generally much less than a linear multiple of the number of cores.
For this analysis, we make the sweeping assumption that using multiple CPUs somewhat more than doubles the performance of a single CPU. That is, we estimate that total computer processing speed increased by a factor of about 4,000 times (= 2.3 x 1,729) from 1989 to 2024.
Computers have a lot more memory
The Prime 750 superminicomputer used by Wilson could have up to 8 MB of RAM (though some installations had only 2 or 4 MB of RAM). A modern desktop PC may have 8 GB of RAM – i.e., 1,024 times as much memory.
Though 8 GB of RAM is quite small for a computer in 2024. For example, the virtual machine we used in our previous article has 128 GB of RAM – that's 16,384 times the maximum memory available in a million dollar computer in 1989.
Computer memory in 2024 is also many times faster than it was in 1989. We assume that the memory speed does not materially change our estimate of CPU speed increase.
Computer costs has plummeted
In this analysis, we're comparing a 1989 superminicomputer with a 2024 desktop PC – because those are the machines that would typically be used for optimization modelling in their respective eras. But this is not an entirely fair comparison, as the superminicomputer cost a million dollars (in today's money), while a high specification desktop computer now costs only a few thousand dollars – a reduction of more than 99%. If we maintained cost parity, then the performance of a 2024 computer would be even greater.
Summary of computer hardware improvements
Compared with 35 years ago, computers are thousands of times faster, with thousands of times more memory, and their cost has fallen by more than 99%.
Solver improvements
Our estimate is based on aggregating separate estimates for periods of time
The best estimate we can find of how much optimization solvers have improved is published by Gurobi. We start with an analysis by Gurobi estimating the computation progress in linear and mixed integer programming from 1991 to 2008. We then look at an updated analysis to 2020, which we extend to 2023.
CPLEX performance improvement: 1991 to 2008

Figure 4 shows Gurobi's assessment of speed improvement for the CPLEX solver when solving MILP models, for each major software version (bars) and cumulative (line), from 1991 to 2008.
The total cumulative speed improvement is a factor of almost 30,000 times faster (note the log scale for the right-hand axis).
Over those 17 years, this equates to about 1.8 times faster per annum, on average. Though improvements don't occur at a steady rate, with especially large improvements occurring in CPLEX versions 2.1-3.0 (inclusion of the dual simplex method) and in CPLEX versions 6.0-6.5 (many improvements gleaned from "mining" the academic literature).
Importantly, this estimate is just the improvement in solver software performance, not allowing for the speed increase of computer hardware over the same period.
Note that we ignore any improvement in solver performance from 1989 to 1991, as we don't have that information. But if the same rate of improvement (1.8 times per annum) had occurred in those 3 years, then we would have another factor of almost 6 times faster.
Gurobi performance improvement: 2009 to 2023
Dr. Bixby, one of the founders of Gurobi, presented an updated analysis of solver performance improvement in 2021, as shown in Figure 5.

The figure states a cumulative improvement factor of 3,730,625 times, from CPLEX 1.2 to Gurobi 9.1 (released in 2020). Given the CPLEX improvement factor of 29,530 above, this implies an additional improvement for Gurobi of 126 times for the period 2009 to 2020.
Subsequent versions of Gurobi claim performance improvements for MILP models of:
Combining these changes, we estimate that from 2009 to 2023 the Gurobi solver's speed improved by a factor of about 178 times.
A factor of 178 over 14 years equates to an average rate of about 1.45 times per annum. This is lower than the 1.8 times annual average rate from 1991 to 2009, but it is still impressive nonetheless.
Solver performance improvement: 1989 to 2024
Overall, by combining each of the solver-related steps above, we can estimate the cumulative improvement in solver performance over the last 35 years.
The result is that MILP solver performance improved by a factor of 5 million times (in round numbers) from 1989 to 2024. This is conservative estimate, as we exclude any improvement that may have occurred from 1989 to 1991, and from 2023 to 2024.
This improvement, assuming the same computer hardware, is equivalent to a model that takes 60 seconds to solve in 2023 taking 10 years to solve if started in 1989. That is, if it was possible to solve at all in 1989.
Note that our solver performance increase estimate is based on the commercial solvers CPLEX and Gurobi. An open-source solver, like HiGHS, is generally not as fast as CPLEX or Gurobi – perhaps by an order of magnitude, more-or-less, depending on the model. Though that hardly seems significant, given the magnitude of speed improvements over the past three+ decades.
Solver + computer performance improvement: 1989 to 2024
Solving MILP models is about 20 billion times faster than it was 35 years ago.
Combined result
Combining the computer hardware speed increase of 4,000 times with the solver software performance improvement of 5 million times, the total improvement from 1989 to 2024 is a factor of 20 billion times faster!
At that rate, a model that takes 60 seconds to solve in 2023 would have taken 38,000 years to solve if started in 1989.
A grain of salt
Of course, we shouldn't take these estimates too literally.
Firstly, there's substantial room for variation in our estimates. Some numbers are uncertain, while others are simply guesses. Also, aggregating the various factors in a multiplicative manner may not be entirely valid.
Secondly, there are many elements that contribute to how fast, or even whether, a MILP model can be solved, in addition to computer and solver raw speed. Other elements include memory size, programming language features, the fit between solver methodology and a model's specific characteristics, and changes in solver features.
Nonetheless, the magnitude of speed increases we've described in this article surely help in solving larger, more difficult MILP models. A lot.
Conclusion
In this article, we estimate the speed improvement in computer hardware and optimization solver software since 1989. This assessment is motivated by an academic paper by Wilson, published 35 years ago, describing an attempt to compile crossword puzzles using mixed integer linear programming (MILP). That attempt was largely unsuccessful, as the task was beyond the capability of MILP solvers at that time.
But both computers and MILP solvers have advanced enormously since 1989 – by a combined factor of around 20 billion time faster! That improvement should be enough to offset at least some of Wilson's pessimism about being able to compile crossword puzzles using MILP models. Likewise for many other optimization models.
In the next article, we attempt to formulate and solve a MILP to compile crossword puzzles. This is still a difficult problem, though given the improvement in computer and solver speed, there is some basis for optimism that the task is now possible.
If you would like help with your own models, then please contact us.
References
The main references used in this article are listed below. Other information is linked within the article.
Bixby, R. 2021. Optimization: Past, Present, Future with Dr. Robert Bixby, YouTube video published by the University of Toronto, accessed 23 December 2023.
Gurobi Optimization, 2015. Computational progress in linear and mixed integer programming, accessed 13 December 2023.
Passmark Software, 2023. Single thread CPU performance, accessed 13 December 2023.
Rupp, K., 2023. Microprocessor trend data, accessed 13 December 2023.
Wilson, J.M., 1989. Crossword compilation using integer programming, The Computer Journal, Volume 32, Number 3, Pages 273–275.