21 September 2022

In this article we continue the Python Production mix series, using the Pyomo library. Specifically, we build Model 6, which changes Model 5 to:
- Declare the model as a Pyomo
pyo.AbstractModel, rather than as apyo.ConcreteModel. - Read the data from a
datfile rather than ajsonfile.
These changes show that, contrary to how abstract and concrete models are portrayed in most blogs, there is actually little difference between abstract and concrete Pyomo models.
5 September 2022

In this article we continue the Python Production mix series, using the Pyomo library. Specifically, we build Model 5, which changes Model 4 to:
- Define the constraints and objective function using
deffunction blocks. - Output the slack values and dual prices (also known as shadow prices) for each constraint.
These changes give us more control over how the model is defined and provide more information about the solution.
16 August 2022

In this article we continue the Python Production mix series, using the Pyomo library. Specifically, we build Model 4, which changes Model 3 to:
- Import the data from an external json file.
- Read the data into the Model object, rather than into separate objects.
These changes reflect features that we may need to include in an operational model.
2 August 2022

In this article we continue the Python Production mix series, using the Pyomo library. Specifically, we build Model 3, which improves Model 2 by:
- Extracting the data from the model, and putting it in an external file.
- Implementing better handling of the solve process.
- Expanding the output to include additional information.
Each of these improvements are important steps in developing a practical design that can be used for operational models.
14 July 2022

In this article we continue the Python Production mix series, using the Pyomo library. Specifically, we build Model 2, which improves Model 1 by extracting the hard coded coefficients and putting them into Python data structures.
Separately the data from the model is an important step in developing a practical design that can be used for operational models.
1 July 2022

In this article we build Model 1 of the Python Production mix series, using the Pyomo library. The Production mix model relates to our hypothetical boutique pottery business, which is described in more detail in the article Python optimization Rosetta Stone.
Our objective for this article is to build and explain the workings of a simple Pyomo example.
Although Model 1 is like many examples of a Pyomo model that you may find on the web and in textbooks, it certainly does not represent best (or even good) practice. In subsequent articles, we'll incrementally improve the model, leading to a structure that is more suitable for operational models.
Even so, Model 1 is an easy-to-understand place to start our exploration of building optimization models in Python. It is worth understanding this model before moving on to more sophisticated versions.
22 June 2022

To start our exploration of optimization modelling in Python, we'll build the same linear programming model using several Python tools. We will, in a sense, develop a Rosetta Stone – with the same model translated into the different "languages" of the Python optimization modelling libraries. Our main purpose is to see how the libraries compare when applied to the same task.
Specifically, we'll replicate the linear program described in our article Production mix via graphical LP. That version of the Production mix model was built in Excel, using Solver/OpenSolver. In this series of articles, we'll build the Production mix model using the Python libraries:
- Pyomo.
- PuLP.
- OR Tools.
- Gekko.
- CVXPY.
- SciPy.
These are, as far as we're aware, the Python libraries that are most used for building linear programming models. Later, we'll add another library, Python MIP, when we use a variety of libraries to build mixed integer programming models.
9 June 2022

A common issue encountered by new Python optimization modellers is setting up a Python environment. There are many libraries that can be used, and some – like Pyomo – require solvers to be installed separately. Getting everything working can be tricky and frustrating.
So, in this article we'll describe the steps we used to set up a new virtual environment, including Python, Jupyter Lab, several optimization modelling libraries, and a selection of solvers. We'll use this environment for subsequent blog articles about building and solving optimization models in Python.
We hope this article helps you create a working Python environment that enables you to replicate our models and build your own models. Note that we are using 64-bit Windows 10, so everything we do is in that context. If you are using a different operating system, then you'll need to adapt the instructions accordingly.
3 June 2022

We're expanding the scope of this blog to include optimization modelling using Python.
Python is a popular programming language for many data science applications, including optimization modelling. A key feature of Python is the availability of many packages for building and solving optimization models, including:
- CVXPY. Modeling language for convex optimization problems.
- Gekko. Modelling language for machine learning and optimization.
- OR-Tools. General purpose linear, mixed integer, and constraint programming, plus specific tools for vehicle routing and graph algorithms.
- PuLP. Optimization modelling language written in Python.
- Pyomo. Optimization modelling language with a diverse set of optimization capabilities.
- Python-MIP. Collection of tools for the modelling and solution of mixed integer linear programs.
- SciPy. General purpose numerical and scientific computing library.
These tools provide access to a variety of solvers, which help us solve a wide range of problem types. In addition to the solvers built into some of the packages, we'll also use:
- Bonmin. A solver for general mixed integer non-linear programs.
- CBC. A linear and mixed integer program solver.
- Couenne. A solver that aims to find global optima of non-convex mixed integer non-linear programs.
- GLPK. Package for solving large-scale linear and mixed integer programs.
- Ipopt. Package for large-scale non-linear optimization.
- NEOS Server. Internet-based service that provides remote access to many solvers.
- Octeract. A global mixed integer non-linear solver.
As discussed in our article Optimization in Excel vs Python, the choice of optimization tool depends on the circumstances, including the model's features and the modellers' and users' familiarity with the tools. As optimization tools, Excel and Python both have advantages and disadvantages. By expanding our blog's scope to include Python tools, we're looking to enable you to use the approach that works best in your situation.
We'll focus on free and open-source packages and solvers, though the concepts can also be applied to commercial software like CPLEX and Gurobi.
In our next article, we'll step through the process of setting up an environment for Python modelling. In subsequent articles, we'll explore a variety of Python optimization packages, sometimes contrasting a Python model implementation with an Excel implementation.
13 May 2022
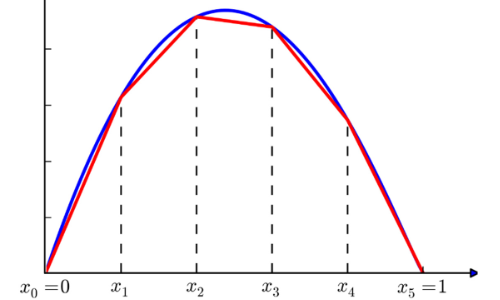
In the real world, we often encounter non-linear relationships in the systems we're modelling. But non-linearities can be difficult to model and even more difficult to solve to optimality.
The recently-published paper "Transformation and linearization techniques in optimization: A state-of-the-art survey" presents a detailed description of transformations and linearizations for a variety of non-linear relationships.
According to the paper's abstract:
To formulate a real-world optimization problem, it is sometimes necessary to adopt a set of non-linear terms in the mathematical formulation to capture specific operational characteristics of that decision problem. However, the use of non-linear terms generally increases computational complexity of the optimization model and the computational time required to solve it.
This motivates the scientific community to develop efficient transformation and linearization approaches for the optimization models that have non-linear terms. Such transformations and linearizations are expected to decrease the computational complexity of the original non-linear optimization models and, ultimately, facilitate decision making.
Asghari et al. (2022). "Transformation and linearization techniques in optimization: A state-of-the-art survey"
The transformation and linearization techniques described in the paper include:
- Multiplication of binary variables.
- Multiplication of binary and continuous variables.
- Multiplication of continuous variables.
- Maximum/minimum operators.
- Absolute value function.
- Floor and ceiling functions.
- Square root function.
- Multiple breakpoint function.
- Piecewise linear approximating functions.
- Log-linearization via Taylor series approximation.
- A new technique for linearizing square root terms by means of transformation.
The detailed descriptions in this paper make a good complement to the booklet MIP formulations and linearizations that we've mentioned previously.
Download the full paper: Transformation and linearization techniques in optimization: A state-of-the-art survey ![]()
If you need help transforming your non-linear model into a linear model, then please contact us.
